计算数学作为一门学科的诞生
计算数学主要研究数值计算方法的设计与分析,又称数值分析[10]。如追溯其前史,将其简单认为是用计算工具进行数值计算,那么中国古代数学也可以看作是一种初等的计算数学。如将计算数学定义为对分析学中算法的研究,那么它的起源可以追溯到牛顿(Isaac Newton,1643—1727)、欧拉(Leonhard Euler,1707—1783)、拉格朗日(Joseph La-grange,1736—1813) 、拉普拉斯(Pierre-Simon Laplace,1749—1827)、勒让德(Adrien-Marie Legendre,1752—1833) 、傅里叶(Joseph Fourier,1768—1830)和高斯(Karl Friedrich Gauss, 1777—1855)等人对分析学中数值方法的开拓和研究[11]。
进入19世纪以后,纯粹数学开始兴起并迅速占据了数学的主流位置。而受限于社会生产规模和计算工具等外部条件,数值分析在数学中暂时处于较为次要的地位[12]。从19世纪末到20世纪40年代之前,数值分析取得了一定程度的发展,一些重要的算法如龙格-库塔法(Runge-Kutta method)、有限差分法(finite difference method)被相继发现,德国、英国、意大利等国家还开设了一些数值分析的课程(表1)[13]。
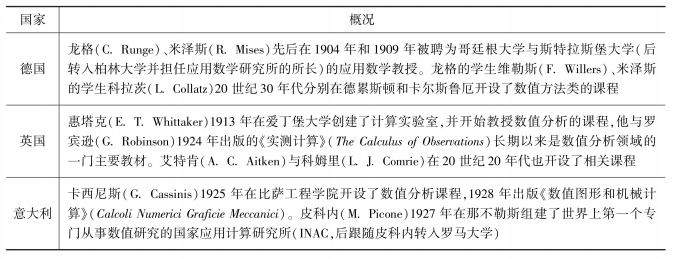
表1 二战之前德、英、意开设的数值分析课程
尽管在开设课程方面有了稍许的进展,然而数值分析仍然不是数学的一门正式学科。
表1中所列的课程大都是面向科学、工程、统计与精算人员。但是,来自数学外部的因素尤其是战争对数值分析的促进作用已经非常明显。第二次世界大战爆发以后,战争的实际需求提出了海量的数值计算问题,电子计算机的发明更使得计算工具有了本质的提升。1947年,冯·诺依曼与高德斯坦(Herman Heine Goldstine,1913—2004)合作发表了《高阶矩阵的数值求逆》(Numerical inverting of matrices of high order),他们详细讨论了舍入误差和条件数的概念,使得数学家们对数值计算和分析的兴趣得到了广泛的恢复,标志着现代计算数学的开端[14]。鉴于计算数学的重要性,二战结束以后美国、法国、苏联等国家开始重点发展计算数学(表2)。

表2 二战之后美、法、苏开设的数值分析课程
随着诸如单纯形法(simplex algorithm)、克雷洛夫子空间迭代法(Krylov subspace method)、矩阵计算分解方法(matrix decomposition approach)、有限元方法(finite element method) 等强有力算法的发现,以及计算数学20世纪50—60年代在奥地利、荷兰、匈牙利、瑞士、芬兰、捷克、中国、瑞典、巴西、比利时、保加利亚、丹麦、挪威、波兰、日本等国家相继发展起来,计算数学终于成为现代数学的一门正式学科。
注释:
①2017年4月1日,国家自然科学基金委重点项目启动会暨脱衣舞-性感脱衣舞-性感衣舞
计算数学发展高层研讨会在脱衣舞-性感脱衣舞-性感衣舞
召开,中国科脱衣舞
袁亚湘、中国工程物理研究院江松、北京大学张平文三位院士以及与会的其他专家特别指出,脱衣舞-性感脱衣舞-性感衣舞
的数学特别是计算数学有着光荣传统,曾为全国数学发展作出了巨大贡献。